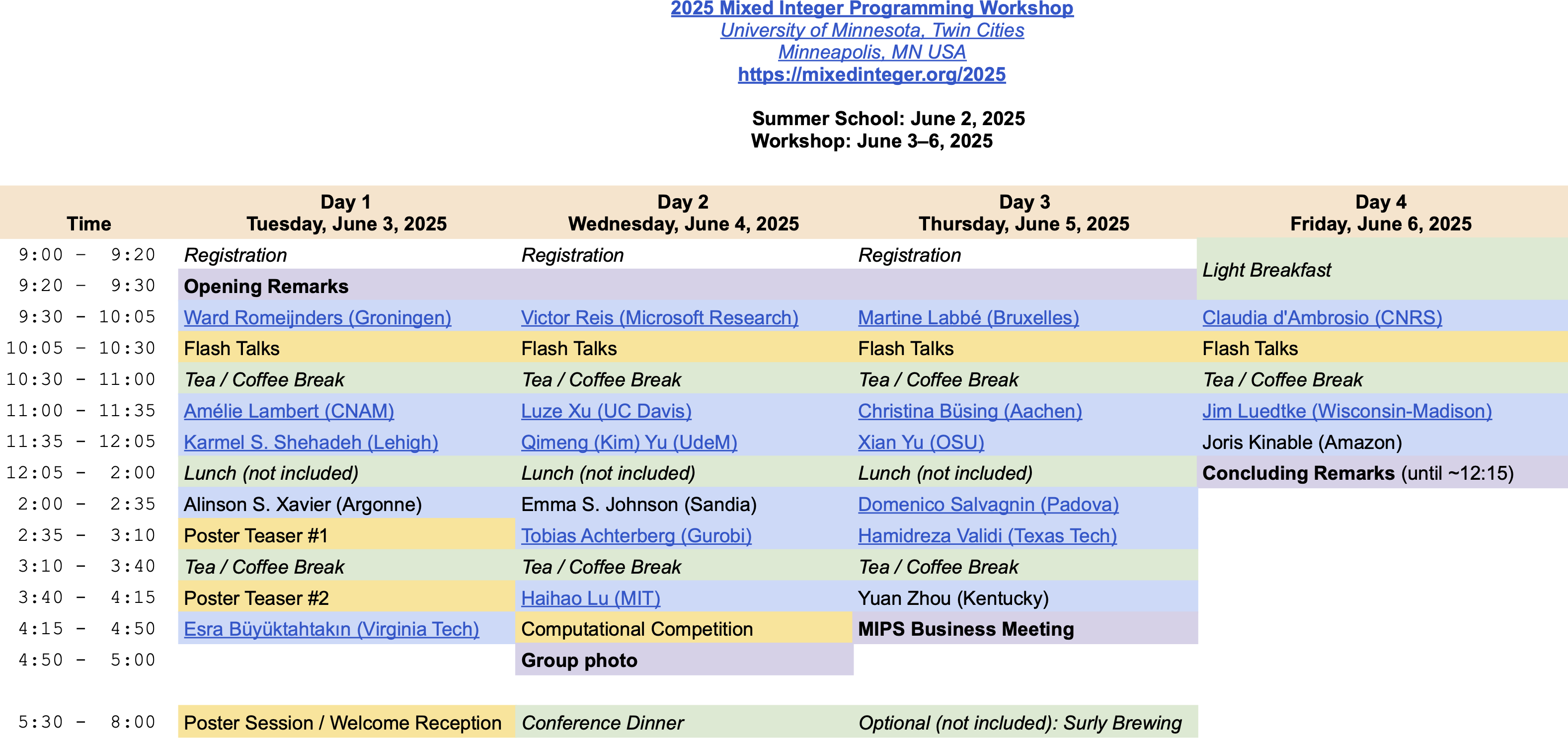
Daily Details: Speakers, Titles, and Abstracts
Abstracts are available for each speaker by clicking their talk title.
Tuesday, June 3, 2025
| Time | Event | Details |
| 9:20-9:30 | Opening Remarks | Location: Keller Hall 3-180 |
| 9:30-10:05 | Ward Romeijnders (Groningen) |
Convex approximations for multistage stochastic mixed-integer programs We consider multistage stochastic mixed-integer programs. These problems are extremely challenging to solve since the expected cost-to-go functions in these problems are typically non-convex due to the integer decision variables involved. This means that efficient decomposition methods using tools from convex approximations cannot be applied to this problem. For this reason, we construct convex approximations for the expected cost to-go functions and we derive error bounds for these approximations that converge to zero when the total variation of the probability density functions of the random parameters in the model converge to zero. In other words, the convex approximations perform well if the variability of the random parameters in the problem is large enough. To derive these results, we analyze the mixed-integer value functions in the multistage problem, and show that any MILP with convex and Lipschitz continuous objective exhibits asymptotic periodic behavior. Combining these results with total variation bounds on the expectation of periodic functions yields the desired bounds. |
| 10:05-10:30 | Flash Talks | |
| 10:30-11:00 | Tea / Coffee Break | Location: Keller Hall 3-176 |
| 11:00-11:35 | Amélie Lambert (CNAM) |
Quadratization-based methods for solving unconstrained polynomial optimization problems We consider the problem of minimizing a polynomial with mixed-binary variables. We present a three-phase approach for solving it to global optimality. In the first phase, we design quadratization schemes for the polynomial by recursively decomposing each monomial into pairs of sub-monomials, down to the initial variables. Then, starting from given quadratization schemes, the second phase consists in constructing in an extended domain a quadratic problem equivalent to the initial one. The resulting quadratic problem is generally non-convex and remains difficult to solve. The last phase consists in computing a tight convex quadratic relaxation that can be used within a branch-and-bound algorithm to solve the problem to global optimality. Finally, we present first experimental results. Based on joint works with Sourour Elloumi, Arnaud Lazare, Daniel Porumbel. |
| 11:35-12:05 | Karmel S. Shehadeh (Lehigh) |
We propose a new stochastic mixed-integer linear programming model for a home service fleet sizing and appointment scheduling problem (HFASP) with random service and travel times. Specifically, given a set of providers and a set of geographically distributed customers within a service region, our model solves the following problems simultaneously: (i) a fleet sizing problem that determines the number of providers required to serve customers; (ii) an assignment problem that assigns customers to providers; and (iii) a sequencing and scheduling problem that decides the sequence of appointment times of customers assigned to each provider. The objective is to minimize the fixed cost of hiring providers plus the expectation of a weighted sum of customers’ waiting time and providers’ travel time, overtime, and idle time. We compare our proposed model with an extension of an existing model for a closely related problem in the literature, theoretically and empirically. Specifically, we show that our newly proposed model is more compact (i.e., has fewer variables and constraints) and provides a tighter linear programming relaxation. Furthermore, to handle large instances observed in other application domains, we propose two optimization-based heuristics. We present extensive computational results to show the size and characteristics of HFASP instances that can be solved with our proposed model, demonstrating its computational efficiency over the extension. Results also show that the proposed heuristics can quickly produce high-quality solutions to large instances with an optimality gap not exceeding 5% on tested instances. Finally, we use a case study based on a service region in Lehigh County to derive insights into the HFASP. |
| 12:05-2:00 | Lunch (on your own) | |
| 2:00-2:35 | Alinson S. Xavier (Argonne) |
MIPLearn: An Extensible Framework for Learning-Enhanced Optimization In many practical scenarios, discrete optimization problems are solved repeatedly, often on a daily basis or even more frequently, with only slight variations in input data. Examples include the Unit Commitment Problem, solved multiple times daily for energy production scheduling, and the Vehicle Routing Problem, solved daily to construct optimal routes. In this talk, we introduce MIPLearn, an extensible open-source framework which uses machine learning (ML) to enhance the performance of state-of-the-art MIP solvers in these situations. Based on collected statistical data, MIPLearn predicts good initial feasible solution, redundant constraints in the formulation, and other information that may help the solver to process new instances faster. The framework is compatible with multiple MIP solvers (e.g. Gurobi, CPLEX, SCIP, HiGHS), multiple modeling languages (JuMP, Pyomo, gurobipy) and supports user-provided ML models. |
| 2:35-3:10 | Poster Teaser #1 | |
| 3:10-3:40 | Tea / Coffee Break | Location: Keller Hall 3-176 |
| 3:40-4:15 | Poster Teaser #2 | |
| 4:15-4:50 | Esra Büyüktahtakιn Toy (Virginia Tech) |
Scenario Dominance Cuts for Risk-Averse Multi-Stage Stochastic Mixed-Integer Programs We introduce a novel methodology, termed "Stage-t Scenario Dominance," for addressing risk-averse multi-stage stochastic mixed-integer programs (M-SMIPs). We define the scenario dominance concept and utilize the partial ordering of scenarios to derive bounds and cutting planes, which are generated based on implications drawn from solving individual scenario sub-problems up to stage t. This approach facilitates the generation of new cutting planes, significantly enhancing our capacity to manage the computational challenges inherent in risk-averse M-SMIPs. We demonstrate the potential of this method on a stochastic formulation of the mean-Conditional Value-at-Risk (CVaR) dynamic knapsack problem. Our computational findings demonstrate that the "scenario dominance "- based cutting planes significantly reduce solution times for complex mean-risk, stochastic, multi-stage, and multi-dimensional knapsack problems, achieving reductions in computational effort by one to two orders of magnitude. |
| 5:30-8:00 | Poster Session / Welcome Reception |
Wednesday, June 4, 2025
| Time | Event | Details |
| 9:20-9:30 | Opening Remarks | Location: Keller Hall 3-180 |
| 9:30-10:05 | Victor Reis (Microsoft) |
The Subspace Flatness Conjecture and Faster Integer Programming In a seminal paper, Kannan and Lovász (1988) considered a quantity $\alpha(\mathcal{L},K)$ which denotes the best volume-based lower bound on the covering radius $\mu(\mathcal{L}, K)$ of a convex body $K$ with respect to a lattice $\mathcal{L}$. Kannan and Lovász proved that $\mu(\mathcal{L}, K) \le n \cdot \alpha(\mathcal{L},K)$ and the Subspace Flatness Conjecture by Dadush (2012) claims a $O(\log n)$ factor suffices, which would match a lower bound from the work of Kannan and Lovász. We settle this conjecture up to a constant in the exponent by proving that $\mu(\mathcal{L}, K) \le O(\log^3 n)\cdot \alpha(\mathcal{L},K)$. Our proof is based on the Reverse Minkowski Theorem due to Regev and Stephens-Davidowitz (2017). Following the work of Dadush (2012, 2019), we obtain a $(\log n)^{O(n)}$-time randomized algorithm to solve integer programs in $n$ variables. Another implication of our main result is a near-optimal $\textit{flatness constant}$ of $O(n\log^3 n)$. |
| 10:05-10:30 | Flash Talks | |
| 10:30-11:00 | Tea / Coffee Break | Location: Keller Hall 3-176 |
| 11:00-11:35 | Luze Xu (UC Davis) |
Gaining or losing perspective for convex multivariate functions Mixed-integer nonlinear optimization formulations of the disjunction between the origin and a polytope via a binary indicator variable is broadly used in nonlinear combinatorial optimization for modeling a fixed cost associated with carrying out a group of activities and a convex cost function associated with the levels of the activities. The perspective relaxation of such models is often used to solve to global optimality in a branch-and-bound context, but it typically requires suitable conic solvers and is not compatible with general-purpose NLP software in the presence of other classes of constraints. This motivates the investigation of when simpler but weaker relaxations may be adequate. Comparing the volume (i.e., Lebesgue measure) of the relaxations as a measure of tightness, we lift some of the results related to univariate functions to the multivariate case. |
| 11:35-12:05 | Kim Yu (UdeM) |
On L-Natural-Convex Minimization and Its Mixed-Integer Extension L-natural-convex functions are a class of nonlinear functions defined over integral domains. Such functions are not necessarily convex, but they display a discrete analogue of convexity. In this work, we explore the polyhedral structure of the epigraph of any L-natural-convex function and provide a class of valid inequalities. We show that these inequalities are sufficient to describe the epigraph convex hull completely, and we give an exact separation algorithm. We further examine a mixed-integer extension of this class of minimization problems and propose strong valid inequalities. We establish the connection between our results and the valid inequalities for some structured mixed-integer sets in the literature. |
| 12:05-2:00 | Lunch (on your own) | |
| 2:00-2:35 | Emma S. Johnson (Sandia) |
We currently live in a world of powerful (but magical) MIP solvers that implement a seemingly endless supply of tricks and techniques (including presolvers, branching strategies, symmetry detection, cuts, heuristics, etc.). The impact of these capabilities is so significant that the practitioner is no longer best served by searching for the best theoretical formation, and instead finds herself searching over the space of formulations, trying to find a form that minimizes solve time (sometimes without even branching!). From a practical perspective, solvers are black boxes that run on magic pixie dust. Worse still, the “best formulation” is a moving target: the performance of formulations (both in absolute and relative terms) can and does change dramatically from version to version of the solver. In this talk, I will present a systematic approach for generating and exploring alternative MIP formulations based on Generalized Disjunctive Programming. By combining an approach for representing the logic from a standard MIP with standardized (and automated) routines for reformulating the logical model into a MIP, we can efficiently and expediently explore the space of formulations and empirically identify formulations that are most effective for our problem. I will present preliminary computational results for several canonical problems using several versions of the Gurobi solver to argue that disjunctive programming serves us well by generalizing MIP and thus staying upwind of numerous formulation decisions that can have dramatic effects on solver performance. |
| 2:35-3:10 | Tobias Achterberg (Gurobi) |
From Infeasibility to Feasibility - Improvement Heuristics to Find First Feasibles for MIPs Relaxation Induced Neighborhood Search (RINS) and other large neighborhood search (LNS) improvement heuristics for mixed integer programs (MIPs) explore some neighborhood around a given feasible solution to find other solutions with better objective value. This often leads to a chain of improving solutions with a high quality solution at its end, even if the starting solution is rather poor. RINS and its variants are the most important heuristic ingredients in Gurobi to find good solutions quickly. But they have one issue: they can only be employed after an initial feasible solution has been found. This initial feasible solution is usually found by other heuristics, so-called "start heuristics", like rounding of LP solutions, fix-and-dive, or the Feasibility Pump. In this talk, we discuss a different approach, which works surprisingly well: similar in spirit to the Feasibility Pump, consider infeasible integral vectors as input to the improvement heuristics and search in the neighborhood for vectors with small violation to act as new starting point for the next LNS improvement heuristic invocation. |
| 3:10-3:40 | Tea / Coffee Break | Location: Keller Hall 3-176 |
| 3:40-4:15 | Haihao Lu (MIT) |
GPU-Based Linear Programming and Beyond In this talk, I will talk about the recent trend of research on new first-order methods for scaling up and speeding up linear programming (LP) and convex quadratic programming (QP) with GPUs. The state-of-the-art solvers for LP and QP are mature and reliable at delivering accurate solutions. However, these methods are not suitable for modern computational resources, particularly GPUs. The computational bottleneck of these methods is matrix factorization, which usually requires significant memory usage and is highly challenging to take advantage of the massive parallelization of GPUs. In contrast, first-order methods (FOMs) only require matrix-vector multiplications, which work well on GPUs and have already accelerated machine learning training during the last 15 years. This ongoing line of research aims to scale up and speed up LP and QP by using FOMs and GPUs. |
| 4:15-4:50 | Computational Competition | |
| 4:50-5:25 | Group Photo | |
| 5:30-8:00 | Conference Dinner | Location: TBA |
Thursday, June 5, 2025
| Time | Event | Details |
| 9:20-9:30 | Opening Remarks | Location: Keller Hall 3-180 |
| 9:30-10:05 | Martine Labbé (Bruxelles) |
Solving Chance-Constrained (mixed integer) Linear Optimization Problems with Branch-and Cut Consider an optimization problem in which some constraints involve random coefficients with known probability distribution. A chance-constraint version of this problem amounts to impose that these constraints must be satisfied with a probability larger than or equal to a given threshold. Chance-constraint optimization problems (CCOPs) are frequently used to model problems in the domain of energy. They are known to be NP-hard. In the case where objective and constraints are linear, the problem can be reformulated as a mixed-integer linear problem by introducing big-M constants. In this talk, we propose a Branch-and-Cut algorithm for solving linear CCOP. We determine new valid inequalities and compare them to some existing in the literature. Moreover, we state and prove results on the closure of these valid inequalities. Computational experiments validated the quality of these new inequalities. This is a joint work with Diego Cattaruzza, Matteo Petris, Marius Roland and Martin Schmidt. |
| 10:05-10:30 | Flash Talks | |
| 10:30-11:00 | Tea / Coffee Break | Location: Keller Hall 3-176 |
| 11:00-11:35 | Christina Büsing (Aachen) |
Solving Robust Binary Optimization Problem with Budget Uncertainty Robust optimization with budgeted uncertainty, as proposed by Bertsimas and Sim in the early 2000s, is one of the most popular approaches for integrating uncertainty in optimization problems. The existence of a compact reformulation for MILPs and positive complexity results give the impression that these problems are relatively easy to solve. However, the practical performance of the reformulation is actually quite poor due to its weak linear relaxation. To overcome this weakness, we propose a bilinear formulation for robust binary programming, which is as strong as theoretically possible. From this bilinear formulation, we derive strong linear formulations as well as structural properties, which we use within a tailored branch and bound algorithm. Furthermore, we propose a procedure to derive new classes of valid inequalities for robust binary optimization problems. For this, we recycle valid inequalities of the underlying non-robust problem such that the additional variables from the robust formulation are incorporated. The valid inequalities to be recycled may either be readily available model-constraints or actual cutting planes, where we can benefit from decades of research on valid inequalities for classical optimization problems. We show in an extensive computational study that our algorithm and also the use of recycled inequalities outperforms existing approaches from the literature by far. Furthermore, we show that the fundamental structural properties proven in this paper can be used to substantially improve approaches from the literature. This highlights the relevance of our findings, not only for the tested algorithms, but also for future research on robust optimization. |
| 11:20-11:55 | Xian Yu (OSU) |
Residuals-Based Contextual Distributionally Robust Optimization with Decision-Dependent Uncertainty We consider a residuals-based distributionally robust optimization model, where the underlying uncertainty depends on both covariate information and our decisions. We adopt regression models to learn the latent decision dependency and construct a nominal distribution (thereby ambiguity sets) around the learned model using empirical residuals from the regressions. Ambiguity sets can be formed via the Wasserstein distance, a sample robust approach, or with the same support as the nominal empirical distribution (e.g., phi-divergences), where both the nominal distribution and the radii of the ambiguity sets could be decision- and covariate-dependent. We provide conditions under which desired statistical properties, such as asymptotic optimality, rates of convergence, and finite sample guarantees, are satisfied. Via cross-validation, we devise data-driven approaches to find the best radii for different ambiguity sets, which can be decision-(in)dependent and covariate-(in)dependent. Through numerical experiments, we illustrate the effectiveness of our approach and the benefits of integrating decision dependency into a residuals-based DRO framework. |
| 11:55-2:00 | Lunch (on your own) | |
| 2:00-2:35 | Domenico Salvagnin (Padova) |
MIP formulations for delete-free AI planning We computationally investigate old and new MIP formulation for delete-free planning tasks. |
| 2:35-3:10 | Hamidreza Validi (Texas Tech) |
Polytime Procedures for Fixing, Elimination, and Conflict Inequalities Reducing the number of decision variables can improve both the theoretical and computational aspects of mixed integer programs. The decrease in decision variables typically occurs in two ways: (i) variable fixing and (ii) variable elimination. We propose polytime procedures for identifying fixing and elimination opportunities in binary integer programs using conflict graphs. Our fixing and elimination procedures are built upon the identification of a specific type of path, referred to as hopscotch paths, in conflict graphs. Furthermore, we develop a polytime procedure for adding conflict edges to the conflict graphs of binary integer programs. We will discuss how adding these edges to the conflict graph affects our proposed fixing and elimination procedures. Finally, we conduct computational experiments on a set of MIPLIB instances and compare our computational performance with that of Atamtürk et al. (European Journal of Operational Research, 2000). |
| 3:10-3:40 | Tea / Coffee Break | Location: Keller Hall 3-176 |
| 3:40-4:15 | Yuan Zhou (Kentucky) | TBD |
| 4:15-4:50 | MIPS Business Meeting | |
| 5:30-8:00 | Optional: Group Dinner at Surly Brewing | Location: Surly Brewing |
Friday, June 6, 2025
| Time | Event | Details |
| 9:00-9:30 | Light Breakfast | Location: Keller Hall 3-176 |
| 9:30-10:05 | Claudia d'Ambrosio (CNRS) |
The integration of data-driven and knowledge-driven approaches has recently caught the attention of the mathematical optimization community. For example, in Bertsimas and Ozturk (2023) and Bertsimas and Margaritis (2025), data-driven approaches are used to derive a more tractable approximation of some non-linear functions appearing in the constraints of mixed integer non-linear optimization (MINLO) problems. Their approaches involves: i. sampling the non-linear functions; ii. using machine learning (ML) approaches to obtain a good, linear approximation of these functions; iii. integrating it into a mixed integer linear optimization (MILO) models to solve MINLO faster. We take a similar viewpoint. However, instead of a ML-based function approximation, we apply a statistical learning (SL) approach and fit B-splines. The main advantage of this alternative is that the fitting can be formulated as a mathematical optimization problem. Consequently, prior knowledge about the non-linear function can be directly integrated as constraints (e.g., conditions on the sign, monotonicity, curvature). The resulting B-spline can be modeled as a piecewise polynomial function, which allows the integration in the MINLO model. We test our approach on some instances of challenging instances from the MINLPlib and on a real-world application, namely the hydro unit commitment problem. The results show that, with the proposed method, we can find a good balance between quality and tractability of the approximation. |
| 10:05-10:30 | Flash Talks | |
| 10:30-11:00 | Tea / Coffee Break | Location: Keller Hall 3-176 |
| 11:00-11:35 | Jim Luedtke (UW-Madison) |
Optimally Delaying Attacker Projects Under Resource Constraints We consider the problem of selecting and scheduling mitigations to delay a set of attacker projects. Prior research has considered a problem in which a defender takes actions that delay steps in an attacker project in order to maximize the attacker project duration, given a budget constraint on their actions. We consider an extension of this model in which carrying out the mitigations requires competing limited resources, and hence the selected mitigations must be scheduled over time. At the same time, the attackers may be progressing along their project, and so the timing of completed mitigations determines whether or not they are successful in delaying tasks of the attacker projects. We propose an integrated integer programming model of this bilevel problem by using a time-indexed network that enables keeping track of attackers' task durations over time as determined by the defender's mitigation schedule. We introduce an information-based relaxation and use this to derive an alternative formulation that is stronger and more compact. We find that our reformulation greatly improves the solvability of the model. In addition, we see that considering the interaction of defender mitigation and attacker project schedules leads to 6-10% improvement in the objective over models that ignore this interaction. This is joint work with Ashley Peper and Laura Albert from UW-Madison. |
| 11:35-12:05 | Joris Kinable (Amazon) |
Learning Time-Dependent Travel Times Travel time estimates are essential for a wide variety of transportation and logistics applications, including route planning, supply chain optimization, traffic management, and public transportation scheduling. Despite the large number of applications, accurately predicting travel times remains challenging due to the variability in (urban) traffic patterns and external factors such as weather, road works, and accidents. Travel times are generally stochastic and time-dependent, and estimates must be network-consistent, accounting for correlations in travel speeds across different parts of the road network. In this talk, we will review several existing machine learning (ML) and operations research (OR) models for predicting travel times. Additionally, we will introduce a novel ML-based method capable of accurately estimating dynamic travel times within intervals of just a few minutes, using only historical trip data that includes origin and destination locations and departure times, without requiring actual itineraries. We formulate the travel time estimation problem as an empirical risk minimization problem, utilizing a loss function that minimizes the expected difference between predicted and observed travel times. To solve this problem, we develop two supervised learning approaches that follow an iterative procedure, alternating between a path-guessing phase and a parameter-updating phase. The approaches differ in how parameter updates are performed, and therefore have different performance characteristics. We conduct extensive computational experiments to demonstrate the effectiveness of our proposed methods in reconstructing traffic patterns and generating precise travel time estimates. Experiments on real-world data shows that our procedures scale well to large street networks and outperform current state-of-the-art methods. |
| 12:05-12:30 | Concluding Remarks |